Premesse
Sin dai tempi antichi l’Uomo ha sempre desiderato di poter raggiungere la perfezione delle cose, la bellezza dell’essere, l’armonia geometrica e per questo è diventato osservatore del sistema che lo circondava.
Ma cos’è la bellezza?
Perchè esiste?
Perchè una cosa sembra bella ed un’altra no?
È nell’occhio di chi guarda, quindi soggettiva, o è ancorata a canoni classici?
E che rapporto c’è tra la bellezza umana e quella di un dipinto o di un paesaggio?
Generalità
Il nostro cervello mostrerebbe una naturale preferenza verso linee e forme disegnate che richiamano un rapporto matematico.
Gli esempi? Sotto i nostri occhi.
Non solo i canoni estetici dominanti obbediscono religiosamente a quelle proporzioni, ma anche i paesaggi naturali, i petali dei fiori, i colori delle piume degli uccelli, la forma delle conchiglie. Il segreto della bellezza universale sarebbe tutto concentrato in una formula: 1:1,618, altrimenti detto “rapporto aureo” esempio di unione perfetta tra Arte e Scienza e semplificato da due linee di grandezza diversa. La natura ha le sue leggi, la Scienza ha lo scopo di spiegarle e quindi di rispondere a tutti i perchè e l’arte ha il compito di descriverle.
Consideriamo un "rettangolo aureo", ovvero un rettangolo le cui dimensioni siano in rapporto aureo. Fig.
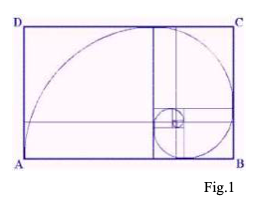 Se si traccia un segmento parallelo al lato "corto" del rettangolo in modo tale da ottenere un quadrato, il rettangolo che resta è ancora un rettangolo aureo, ovvero il segmento tracciato divide il lato lungo del rettangolo in due segmenti che sono in proporzione aurea e sono separati da un "punto aureo".
Se si traccia un segmento parallelo al lato "corto" del rettangolo in modo tale da ottenere un quadrato, il rettangolo che resta è ancora un rettangolo aureo, ovvero il segmento tracciato divide il lato lungo del rettangolo in due segmenti che sono in proporzione aurea e sono separati da un "punto aureo".
Facendo la stessa operazione con questo rettangolo più piccolo si ottiene un nuovo quadrato, un nuovo rettangolo aureo e due nuovi punti aurei. (Fig.2)
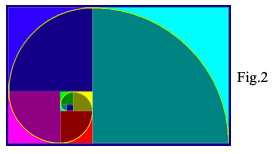
Immaginiamo di andare avanti "all'infinito" e di unire i punti aurei (seguendo ad esempio il verso orario) con un curva che sia ogni volta tangente al segmento che tocca nel punto aureo. Quella che otterremo è una spirale logaritmica.

L'elemento comune di tutte figure è rappresentato dalla spirale logaritmica detta anche "spirale aurea", attraverso la quale lo sviluppo armonico della forma è legato alla necessità degli esseri viventi di accrescere "secondo natura" in maniera ottimale e meno dispendiosa possibile. (Figg. 3, 4, 5, 6)
Sezione aurea nell’arte e nella architettura
Il rapporto aureo o “rapporto divino” è uno dei sistemi più antichi usati per dare proporzione agli oggetti. Sembra che già nell’antico Egitto e in Babilonia lo si conoscesse, esso era noto anche presso i Greci, che lo consideravano come un valore proporzionale ideale.
Durante l’epoca del Rinascimento Italiano, il grande Leonardo da Vinci e pittori come Bernardo Luini, Sandro Botticelli, Piero della Francesca, usavano la sezione aurea nelle loro opere mentre, scultori greci come Policleto. Miron, Fidia, scoprirono il “sistema delle proporzioni ideali” del corpo umano.
Gli studi di Leonardo Da Vinci sul corpo umano hanno indicato come Rapporto Aureo il rapporto esteticamente più piacevole tra le lunghezze del corpo umano (ad esempio tronco/gambe):
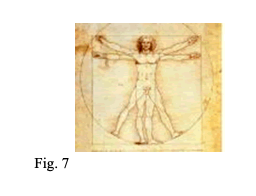
"Nessuno capiva meglio di Leonardo da Vinci la divina struttura del corpo umano. Leonardo disseppelliva i corpi per misurare le proporzioni esatte della struttura ossea umana. Fu il primo a mostrare che il corpo umano è letteralmente costituito di elementi che stanno tra loro in rapporto di phi." Stabilì che le proporzioni
umane sono perfette quando l'ombelico divide l'uomo in modo
aureo. (Fig. 7)
 Nella Gioconda (fig. 8) il rapporto aureo è stato individuato: nella disposizione del quadro nelle dimensioni del viso nell’area che va dal collo a sopra le mani in quella che va dalla scollatura dell’abito fino a sotto le mani.
Nella Gioconda (fig. 8) il rapporto aureo è stato individuato: nella disposizione del quadro nelle dimensioni del viso nell’area che va dal collo a sopra le mani in quella che va dalla scollatura dell’abito fino a sotto le mani. La sezione aurea affascinò altri pittori, come Botticelli (1445-1510) e la rappresentò ne La Venere. Infatti misurando l’altezza da terra dell’ombelico e l’altezza complessiva il loro rapporto risulterà 0.618, così anche il rapporto tra la distanza tra il collo del femore e il ginocchio e la lunghezza dell’intera gamba o anche il rapporto tra il gomito e la punta del dito medio e la lunghezza del braccio. (Fig. 9)
La sezione aurea affascinò altri pittori, come Botticelli (1445-1510) e la rappresentò ne La Venere. Infatti misurando l’altezza da terra dell’ombelico e l’altezza complessiva il loro rapporto risulterà 0.618, così anche il rapporto tra la distanza tra il collo del femore e il ginocchio e la lunghezza dell’intera gamba o anche il rapporto tra il gomito e la punta del dito medio e la lunghezza del braccio. (Fig. 9)
 Il numero phi è presente anche nelle dimensioni architettoniche del Partenone. (Fig. 10)
Il numero phi è presente anche nelle dimensioni architettoniche del Partenone. (Fig. 10)

Il Rapporto Aureo
Un largo contribuito, alla conoscenza ed alla divulgazione di questo metodo di suddivisione armonica, è stato dato dal matematico Luca Pacioli con la pubblicazione del libro “La divina proporzione”, illustrato con i disegni di Leonardo.
Nel XIX° secolo il tedesco Zeising portò avanti un importante e impegnativo lavoro scientifico misurando circa 2.000 corpi umani e arrivando alla conclusione che i corpi più armoniosi rispecchiavano il Rapporto Aureo.
Si può affermare pertanto che fin dai tempi più antichi la “proporzione divina” veniva sempre presa in considerazione per ottenere la dimensione armonica delle cose: dalla geometria all'architettura, dalla pittura alla musica, fino alla natura del creato possiamo osservare come tali rappresentazioni spesso rispettino un rapporto pari a 1,618, che non a caso è stato definito numero d'oro.
Quindi “rapporto aureo” è sinonimo di bellezza, di funzionalità, di armonia. Si sa che essere belli permette di avere una esistenza più felice: vita sentimentale più intensa, numerose amicizie, carriere in ascesa e maggiori guadagni. Ecco spiegata l’ossessione del fitness, la mania del chirurgo estetico, le iscrizioni alle palestre.
Cos’è il Rapporto Aureo?
È il rapporto geometrico tra due entità a e b, tale che:
(a+b) : a = a : b
Cioè il rapporto fra le lunghezze delle due parti è uguale al rapporto fra la lunghezza dell’intero segmento e quella della parte più lunga. Per spiegare meglio tutto questo facciamo qualche esempio:
- prendiamo un segmento C
- dividiamolo in due parti a e b così che la parte maggiore sia media proporzionale tra la parte minore e la somma delle due.
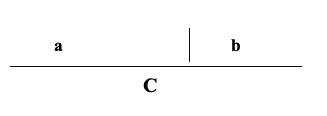 Il valore numerico di detta proporzione è 0,618 per a=1, mentre è 1,618033 per b=1 “numero d’oro” indicato con la lettera ”ϕ “ in onore di Fidia.
Il valore numerico di detta proporzione è 0,618 per a=1, mentre è 1,618033 per b=1 “numero d’oro” indicato con la lettera ”ϕ “ in onore di Fidia.
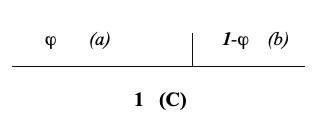 Possiamo vedere che esistono due numeri la cui differenza è uguale a 1 e tali che 1: 0,618 =1,618 .(Fig. 11)
Possiamo vedere che esistono due numeri la cui differenza è uguale a 1 e tali che 1: 0,618 =1,618 .(Fig. 11)
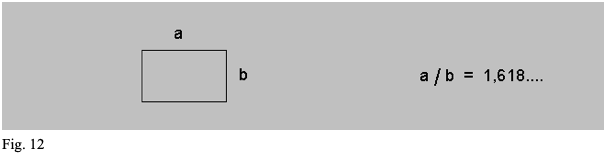
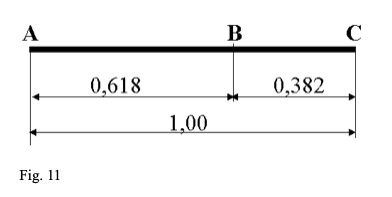 Gli antichi greci (filosofi, matematici e architetti) avevano già risolto questo dilemma: il rapporto fra il lato lungo a e il lato corto b, per ottenere un’immagine estetica, deve essere uguale a 1,618 (fig. 12):
Gli antichi greci (filosofi, matematici e architetti) avevano già risolto questo dilemma: il rapporto fra il lato lungo a e il lato corto b, per ottenere un’immagine estetica, deve essere uguale a 1,618 (fig. 12):
 Il numero PHI parte dalla sequenza di uno scopritore duecentesco, Leonardo Pisano, detto Fibonacci che identificò una successione numerica con proprietà particolari e curiose. La proprietà matematica di questa successione è che ogni elemento (a partire dal secondo) è uguale alla somma dei due precedenti. Usando questa formula è possibile estendere la sequenza all'infinito.
La sequenza inizia con 1,1,2,3,5,8,13,21,34,55,89,144,233, etc…(Fig. 13)
Il numero PHI parte dalla sequenza di uno scopritore duecentesco, Leonardo Pisano, detto Fibonacci che identificò una successione numerica con proprietà particolari e curiose. La proprietà matematica di questa successione è che ogni elemento (a partire dal secondo) è uguale alla somma dei due precedenti. Usando questa formula è possibile estendere la sequenza all'infinito.
La sequenza inizia con 1,1,2,3,5,8,13,21,34,55,89,144,233, etc…(Fig. 13)
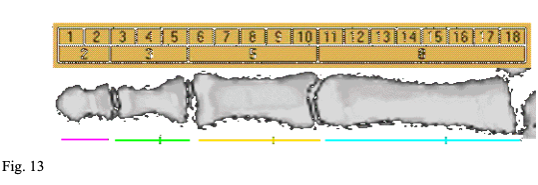 La sequenza ha un'altra proprietà matematica interessante, che si può notare calcolando il rapporto di ogni elemento con quello precedente. Partendo dai primi due elementi, il rapporto è 1 - 1, o semplicemente 1. Il secondo rapporto è 2 - 1, o 2. Il terzo è 3 - 2, o 1,5; il quarto è 5 - 3 o circa 1,67; il quinto è 8 - 5, o 1,6. Gli altri sono 1,625, circa 1,615, circa 1,619, circa 1,618.
La sequenza ha un'altra proprietà matematica interessante, che si può notare calcolando il rapporto di ogni elemento con quello precedente. Partendo dai primi due elementi, il rapporto è 1 - 1, o semplicemente 1. Il secondo rapporto è 2 - 1, o 2. Il terzo è 3 - 2, o 1,5; il quarto è 5 - 3 o circa 1,67; il quinto è 8 - 5, o 1,6. Gli altri sono 1,625, circa 1,615, circa 1,619, circa 1,618.
Nel settecento si scoprì che questi rapporti convergono su un numero irrazionale detto phi, i cui primi termini sono 1,618034. (più precisamente, phi è 1/2 della radice quadrata di 5 più 1/2). Questo significa che ogni numero è circa 1,618034 volte più grande del numero che lo precede.
Al rapporto fra le parti, così come matematizzato nella sezione aurea e nella successione di Fibonacci, la geometria della natura fa costantemente appello. L’esempio abitualmente citato viene tratto dal mondo delle piante, e precisamente dalla fillotassi (disposizione delle foglie attorno ai rami e dai rami attorno al tronco, nonché dei petali e dei semi) dove la disposizione proiettata nel piano, disegna spirali che si ampliano nelle armoniose volute sottese alla regola d’oro.
Per quanto concerne il mondo zoologico, si è adusi far menzione alla conchiglia dei molluschi che, nell’accrescersi, registra il proprio passato:
“la forma è il risultato della crescita, la crescita è l’espressione di una formula”
PHI e l’uomo
- Se moltiplichiamo per 1,618 la distanza che, in una persona adulta proporzionata va dai piedi all'ombelico, otteniamo la sua statura. La distanza che va dal ginocchio all'anca, moltiplicata per il numero d'oro, dà la lunghezza della gamba, dall'anca al malleolo. (Fig. 14)
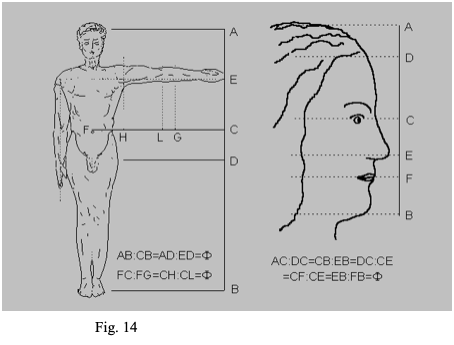
- la distanza dal gomito alla mano (con le dita tese), moltiplicata per 1,618, dà la lunghezza totale del braccio. (Fig. 15)
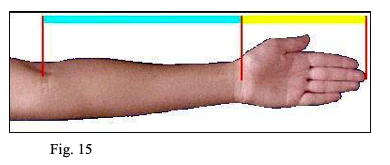
- i rapporti tra le falangi delle dita medio e anulare sono aurei, così il volto umano è tutto scomponibile in una griglia i cui rettangoli hanno i lati in rapporto aureo. (Fig. 16)
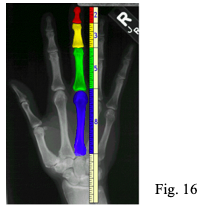
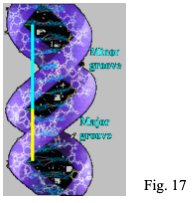
- La molecola di DNA si muove a spirale in proporzione di phi: essa misura 24 angstrom in lunghezza e 21 angstrom in larghezza per ogni ciclo della sua duplice elica spirale. 34 e 21 chiaramente sono numeri della serie di Fibonacci ed il loro rapporto di 1,6190476 è vicino al rapporto phi 1.6180339. (Fig. 17)
Nella figura a fianco possiamo individuare numerosi rapporti aurei (fig 18):

A/a= tra l'altezza e larghezza del viso.
B/b= posizione della linea degli occhi rispetto al mento ad alla fronte.
C/d= posizione della bocca rispetto
al mento ed agli occhi.
D/d= altezza e larghezza del naso.
E/e= lunghezza ed altezza del profilo della bocca.
F/f= larghezza degli occhi e la loro distanza.
H/h= distanza degli occhi rispetto al centro di simmetria del viso.
In un segmento, si fissi un punto intermedio in modo che lo divida in parti diseguali. Le parti sono dette in Rapporto Aureo se la parte più corta è proporzionata alla più lunga allo stesso modo della parte lunga rispetto all’intero segmento.
Basti pensare alla struttura anatomica del piede dove le due parti diseguali o segmenti sono rappresentate da (fig. 19):
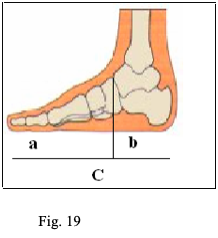
- retropiede o parte b (segmento più corto)
- avampiede o parte a (segmento più lungo)
- piede o parte C (segmento completo)
Se misurando i due segmenti a e b (Rx, strumenti chirurgici…) e applicando la formula:
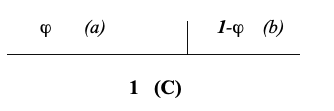
Si ottiene il rapporto 1,618 allora possiamo dire che il piede in esame è proporzionale, funzionale ed esteticamente bello. Per quanto concerne più da vicino, cioè nell’apparato di moto, è stato rilevato che il numero d’oro è il valore del rapporto fra il piano della sezione massima della coscia e la superficie plantare del piede rispetto al ginocchio.
La risposta, positiva, è insita nel fondamento geometrico:
- stabilità,
- armonia,
- matematica
vi fanno il loro trionfale ingresso sulla scia dell’alto contenuto in simmetria delle configurazioni elicoidali di moto, là dove il numero d’oro e la serie di Fibonacci sono, per così dire, di casa. Infatti nel corso della meccanica antigravitaria il rapporto fra le rotazioni nel piano trasverso e le rotazioni nel piano frontale tende al valore “aureo”.
Va tenuto presente che, in genere, la quantificazione del rapporto è arrotondata, nella media, a 1:0,5. Trattasi di un dato artificioso, giustificato dall’ampiezza dei limiti morfo-meccanici dell’articolazione cruro-podalica ma che comunque, valutazioni in eccesso o in difetto, non ne inficiano la validità della regola. Considerato che il fulcro della “meccanica antigravitaria” è la trasmissione trasverso-frontale delle rotazioni, pervenire alla sua quantificazione nel singolo caso è, un decisivo passo verso la conoscenza fisio-patologica.
E tutto lascia ritenere che le ricerche in merito fornirà, nell’immediato futuro, i mezzi per l’agevole rilievo, in diagnostica, del rapporto fra le rotazioni nel piano trasverso e le rotazioni nel piano frontale.
“L’universo è unito in modo meraviglioso: il rapporto aureo è il rapporto delle meraviglie” (Davis e Hersch)
Conclusioni
Nel 1225 Fibonacci pubblicò il " Liber quadratorum " dedicato a Federico II che riporta alcuni problemi sottoposti dal Maestro Giovanni risolvibili con equazioni quadrate e cubiche. il "Liber quadratorum" che costituisce un brillante lavoro sulle equazioni indeterminate di 2° grado: un lavoro nel quale è visibile l'influsso della tradizione culturale araba.
Il "Liber Abaci" fu rivisto nel 1228 per essere dedicato a Michele Scoto. In tutta la sua produzione è sicuramente l'opera più importante è un lavoro contenente quasi tutte le conoscenze aritmetiche e algebriche ed ha avuto una funzione fondamentale nello sviluppo della matematica dell'Europa occidentale. In particolare la numerazione indo-arabica, che prese il posto di quella latina semplificando notevolmente i commerci extraeuropei, fu conosciuta in Europa tramite questo libro.
In tale sistema di numerazione, il valore delle cifre dipende dal posto che occupano: pertanto egli fu costretto ad introdurre un nuovo simbolo, corrispondente allo zero "0", per indicare le posizioni vacanti. Il decreto della Repubblica di Pisa gli conferì il titolo di "Discretus et sapiens magister Leonardo Bigollo" a riconoscimento dei grandi progressi che apportò alla matematica. Fibonacci morì qualche tempo dopo il 1240, presumibilmente a Pisa.
Anche al giorno d'oggi la fama di Leonardo è tale che esiste un'intera pubblicazione dedicata a questi argomenti: il "Fibonacci Quarterly", periodico matematico dedicato interamente all'aritmetica connessa alla sequenza di Fibonacci.
Bibliografia
- R. Paparella Treccia, L’uomo e il suo moto - dalla deambulazione al tennis, Verduci Editore, pp. 131-135, - 1988.
- R. Paparella Treccia, Il piede dell’uomo, Verduci Editore, Ottobre 1977.
- Fare Matematica, Fascicolo n. 1, Geometria e Arte, ed. BCM.
- Maurizio Bonicatti, Enciclopedia di tutte le arti di tutti i popoli in tutti i tempi, vol. II, pp. 41-51, Fratelli Fabbri Editori, Milano 1974.
- G. Brigola, Annali della fabbrica del Duomo, Milano 1877, vol I, pp. 209–211.
- Giorgio Cricco, Francesco P. Di Teodoro, Itinerario dell’arte, Vol. 1, ed. Zanichelli.
- M. Gaffo, Numeri e cifre (tratto da "Focus" n. 79, Maggio 1999), ed. Mondatori.
- Hans M. Enzensberger, Il mago dei numeri, Einaudi.
- Martin Kemp, La scienza dell’Arte, ed. Giunti.
- Carl Schefold, Collana il Marco Polo (vol. Grecia classica, pp. 131-181).
- E. Vorobyou, I numeri di Fibonacci, Le Monnier .
- J. Wasserman, Leonardo da Vinci, ed. Garzanti.
- AA.VV. Empirical studies of arts, 15:111-255, -1997.
- Green C. D. All That Glitters: A Review of Psychological Research on the Aesthetics of the Golden Section. Perception, 24, 937-968, -1995.
- Hoge H. The golden section hypothesis – its last funeral. Empirical studies of arts, 15:233-255, -1997.
- Livio M. La sezione aurea, Roma: Rizzoli 2003. le of its double



 Vuoi navigare al meglio dal tuo smartphone?
Vuoi navigare al meglio dal tuo smartphone? 
 Se si traccia un segmento parallelo al lato "corto" del rettangolo in modo tale da ottenere un quadrato, il rettangolo che resta è ancora un rettangolo aureo, ovvero il segmento tracciato divide il lato lungo del rettangolo in due segmenti che sono in proporzione aurea e sono separati da un "punto aureo".
Se si traccia un segmento parallelo al lato "corto" del rettangolo in modo tale da ottenere un quadrato, il rettangolo che resta è ancora un rettangolo aureo, ovvero il segmento tracciato divide il lato lungo del rettangolo in due segmenti che sono in proporzione aurea e sono separati da un "punto aureo".

 Nella Gioconda (fig. 8) il rapporto aureo è stato individuato: nella disposizione del quadro nelle dimensioni del viso nell’area che va dal collo a sopra le mani in quella che va dalla scollatura dell’abito fino a sotto le mani.
Nella Gioconda (fig. 8) il rapporto aureo è stato individuato: nella disposizione del quadro nelle dimensioni del viso nell’area che va dal collo a sopra le mani in quella che va dalla scollatura dell’abito fino a sotto le mani. La sezione aurea affascinò altri pittori, come Botticelli (1445-1510) e la rappresentò ne La Venere. Infatti misurando l’altezza da terra dell’ombelico e l’altezza complessiva il loro rapporto risulterà 0.618, così anche il rapporto tra la distanza tra il collo del femore e il ginocchio e la lunghezza dell’intera gamba o anche il rapporto tra il gomito e la punta del dito medio e la lunghezza del braccio. (Fig. 9)
La sezione aurea affascinò altri pittori, come Botticelli (1445-1510) e la rappresentò ne La Venere. Infatti misurando l’altezza da terra dell’ombelico e l’altezza complessiva il loro rapporto risulterà 0.618, così anche il rapporto tra la distanza tra il collo del femore e il ginocchio e la lunghezza dell’intera gamba o anche il rapporto tra il gomito e la punta del dito medio e la lunghezza del braccio. (Fig. 9) Il numero phi è presente anche nelle dimensioni architettoniche del Partenone. (Fig. 10)
Il numero phi è presente anche nelle dimensioni architettoniche del Partenone. (Fig. 10)
 Il valore numerico di detta proporzione è 0,618 per a=1, mentre è 1,618033 per b=1 “numero d’oro” indicato con la lettera ”ϕ “ in onore di Fidia.
Il valore numerico di detta proporzione è 0,618 per a=1, mentre è 1,618033 per b=1 “numero d’oro” indicato con la lettera ”ϕ “ in onore di Fidia. Possiamo vedere che esistono due numeri la cui differenza è uguale a 1 e tali che 1: 0,618 =1,618 .(Fig. 11)
Possiamo vedere che esistono due numeri la cui differenza è uguale a 1 e tali che 1: 0,618 =1,618 .(Fig. 11) Gli antichi greci (filosofi, matematici e architetti) avevano già risolto questo dilemma: il rapporto fra il lato lungo a e il lato corto b, per ottenere un’immagine estetica, deve essere uguale a 1,618 (fig. 12):
Gli antichi greci (filosofi, matematici e architetti) avevano già risolto questo dilemma: il rapporto fra il lato lungo a e il lato corto b, per ottenere un’immagine estetica, deve essere uguale a 1,618 (fig. 12): Il numero
Il numero  La sequenza ha un'altra proprietà matematica interessante, che si può notare calcolando il rapporto di ogni elemento con quello precedente. Partendo dai primi due elementi, il rapporto è 1 - 1, o semplicemente 1. Il secondo rapporto è 2 - 1, o 2. Il terzo è 3 - 2, o 1,5; il quarto è 5 - 3 o circa 1,67; il quinto è 8 - 5, o 1,6. Gli altri sono 1,625, circa 1,615, circa 1,619, circa 1,618.
La sequenza ha un'altra proprietà matematica interessante, che si può notare calcolando il rapporto di ogni elemento con quello precedente. Partendo dai primi due elementi, il rapporto è 1 - 1, o semplicemente 1. Il secondo rapporto è 2 - 1, o 2. Il terzo è 3 - 2, o 1,5; il quarto è 5 - 3 o circa 1,67; il quinto è 8 - 5, o 1,6. Gli altri sono 1,625, circa 1,615, circa 1,619, circa 1,618.